1. Introduction
I got my TI Voyage 200, a M68k based calculator stopped manufacture at 2013. I don't like these new colored LCD calculators but my good old CASIO FX-9800GII SD lacks a usable CAS program, although I could play Wolfenstein on it.
Before get into the topic I'll introduce a few goodies I found for V200.
2. RPN
Whoever (Lars Frederiksen) wrote this plugin must be a huge HP calculator fan.
There is a bug with APPROX key on
Voyage 200, which makes me learned M68k assembly language, and
disassembled the executable. They I found the code was written in a
messy way or at least complied from C, and the internal model of
TI-89/TI-92+/V200 series uses RPN, so if I want I could probably
came up with a better one later.
This assembly program is very easy to use for entering large expressions. Another flash application you could try is Equation Writer.
3. Calculus made easy
This is paid software, my conclusion is you don't need it if you are the senior calculator programmer. Most of the features are builtin of AMS, the OS running on TI M68k calculators, or easy enough to be implemented in TI-BASIC in a couple hours if you know the method. But if you'll have tests soon this could be a good review guide.
Their software has serial code protection and each code only works for one product ID of calculator. So if your calculator got broken you would lose access to these paid software.
4. Laplace and Z transform
Besides the DiffEq program, there are other Laplace transform programs, this one also has a symbolic circuit solver similar to the features provided by Symbulator. However since this requires an assembly shell to be functional and the source code is not disclosed, Symbulator is still a better choice. And I did a little benchmark and found it surprisingly that this assembly program does not outperform the DiffEq programmed with only interpreted scripts.
5. Symbulator
Not long after I uploaded a version of Symbulator that contains the bug fix I mentioned later in this article, Roberto Perez-Franco, who is the author of the Symbulator program, contacted me about his plan on continuing on the development. Now the latest version is Symbulator 7 in beta phase, with many improvements on its interface compared to version 6, is available from the renewed symbulator.com domain.
The content below should be considered somewhat outdated. Please check the website above for up-to-date documentation and examples.
Finally, into the main topic. The latest and final version is Symbulator 6, a slightly order version from paxm.org on Internet Achieve is Q, where you can also find the DiffEq programs by Lars Frederiksen that is the dependency of Symbulator. Both version are tested and work on V200, and version 6 is definitely superior (despite there is a bug in the lasted version that is still available). There are also many useful programs on that site exclusively, so please checkout them if you are interested in numeric methods and electrical engineering.
The netlist convention is similar to SPICE (while actually I
only used GNUCap which is compatible), except current is not
i but instead j, and voltage is e
rather than v, this is due to these
variable prefixes has special meanings. Symbulator has the symbolic
feature powered by AMS which is impossible with SPICE, and as a
result there is no need for special syntax for dependent
sources.
Remember to run dif\language() before transient
analysis to ensure the variables necessary to run DiffEq are
initialized, especially when you have reset the RAM.
The following sections are based from machine translated thesis in Spanish by Roberto Pérez-Franco on Symbulator, adapted to the latest available release of Symbulator 6 so the differences are explicitly pointed out if you have read the documentation of older version of Symbulator, such as version Q.
5.1. Alternating current analysis
While there are some documentation in English on how to use
Symbulator for DC, and TR analysis is straightforward, there are
not much information on AC with complex number. The gateway is
s\ac(cir,ω).
The capacitors and inductors only have 4 elements in AC analysis, that is, there is no need for initial current/voltage. If the values are already in impedance (Ohm), just use the resistor instead.
Symbulator would use RECTANGULAR
and RADIAN modes for internal
processing but user's configuration would be saved and
restored.
It seems the only available version of Symbulator 6 Beta's AC
function was not complete, as the examples from the thesis cannot
be solved. A workaround for this is to replace the
solve() call in s\s8 to
cSolve(). The context is change from:
|If βtool="fd" or βtool="tr" Then|expr("solve((v"&αζ2&"-v"&αζ3&")/(s)=("&αζ4&")*(i"&αζ1&"-("&αζ5&")/s)+("&ζζ&"),i"&αζ1&")→eq"&αζ1)|Else|expr("solve((v"&αζ2&"-v"&αζ3&")/(ω*ⅈ)=("&αζ4&")*(i"&αζ1&")+("&ζζ&"),i"&αζ1&")→eq"&αζ1)5 |EndIf
To:
|If βtool="fd" or βtool="tr" Then|expr("solve((v"&αζ2&"-v"&αζ3&")/(s)=("&αζ4&")*(i"&αζ1&"-("&αζ5&")/s)+("&ζζ&"),i"&αζ1&")→eq"&αζ1)|Else|expr("cSolve((v"&αζ2&"-v"&αζ3&")/(ω*ⅈ)=("&αζ4&")*(i"&αζ1&")+("&ζζ&"),i"&αζ1&")→eq"&αζ1)5 |EndIf
There could be other improvements to the program, that I might start work on these later.
5.1.1. Display angle in polar form
The V200 comes with ▶Polar command.
However from AMS 3.0 above the result would be given in a less
readable form. For example 3+4𝕚▶Polar gives
.
The s\aa() command gives the more readable polar
angle form. For example s\aa(3+4𝕚) gives 5 ∠ 53.1301024. This command used to be called
absang().
5.1.2. Input data
There is a second parameter for s\ac(circuit,ω),
where ω is the frequency in rad/s
form, and by the hertz form can be converted to this form.
5.1.3. Impedance
It would be just like resistance but in complex numbers.
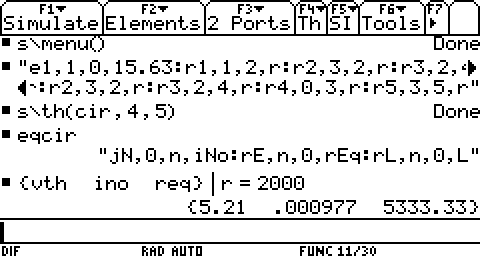
The passive Thevenin analysis has been separated to
another program s\er(cir,n1,n2), the solved equivalent
impedance will be stored in variable zeq. Passive means there is no
current/voltage source in the network.
5.1.4. When things are getting slow
The rule is, whenever you are able to solve it with simple current/voltage divisions in AC and want exact result, it is better just do it by hand.
Symbulator could get very slow when solving complex number equations in exact mode. Another method is use float point number in input so it would run in approximation mode.
Given this netlist:
"e1,1,0,6:r1,1,2,1:r2,2,0,-𝕚:r3,2,3,2:r4,3,0,𝕚""Here we solve for the voltage between 3,0. The math should be easy and only takes
several seconds for the calculator:
But if you dare to solve the netlist directly with
s\ac() in exact mode, after a long time the calculator
would still be busy. If it's in exam then good luck with that.
Fortunately with approximation mode Symbulator solves to
1.38461538+.923076923𝕚 (stored in
vr4), which is indeed correct.
5.2. Frequency domain analysis
The function is s\fd(cir).
Similar to transient analysis, the 5th element of l and c are initial
current and voltage respectively. For Symbulator 6 missing the 5th
element for inductor or capacitor would give an error.
5.3. Expert mode
The function is s\ex(cir). The idea is that once
you have basic understanding of how Symbulator can generate
equations for circuit analysis, you can specify additional unknowns
and constraints and then solve form them. To be honest it is not
that scary.
6. Compare to GNUCap
There isn't much documentation on GNUCap, but since it is a program running on PC it is fast as light compared to the calculator program running with very limited computing power.
For the netlist:
"j1,0,1,2:r1,1,2,5:r2,2,3,8:ca,2,3,625E-6:l1,3,0,25E-3:r3,1,4,2
:l2,4,5,10E-3:r4,4,5,4:r5,5,0,6"The result of s\ac(cir,400) is
1.04-0.31𝕚. To do that in GNUCap, the input file needs
to be like so:
And this is the result:
AC example
#Freq ir(r1) ii(r1)
63.662 1.0402 -0.31048