Lab 11: Complex Numbers TIMS

Table of Contents

1. Introduction
2. Procedures
3. Feedback

1. Introduction

This exercise investigates the relation between complex number and sinusoidal waves. We would define how to convert between sinusoid and magnitude/phase complex number representation, and write a MATLAB program to convert between polar form/rectangular form of complex numbers.

2. Procedures

2.1. Exercise

Figure 1. Conversion to polar form and graph

2.2. Sinusoids as Complex Numbers

2.2.1. Phasor Diagram

Having ARB1 to be $\sin (t)$ and ARB2 to be $\sin (t + 90^{\circ})$ .

Figure 2. ARB1 and ARB2

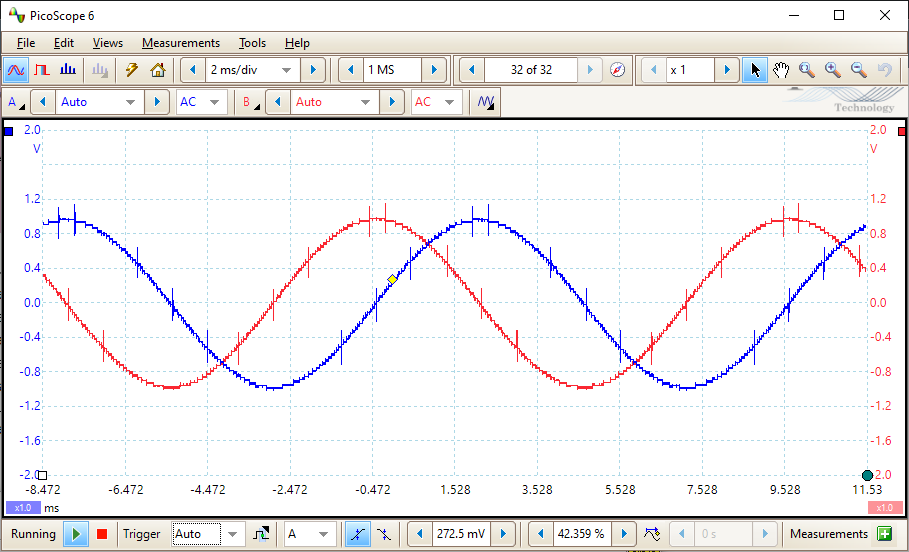
The sum of ARB1 and ARB2 is 1+j or $\sqrt{2} e^{j 45^{\circ}}$ .

If change ARB2 to $\sin (t - 90^{\circ})$ , as in Figure 3, “ARB2 changed phase”, the sum would be 1-j or $\sqrt{2} e^{j - 45^{\circ}}$ .

Figure 3. ARB2 changed phase

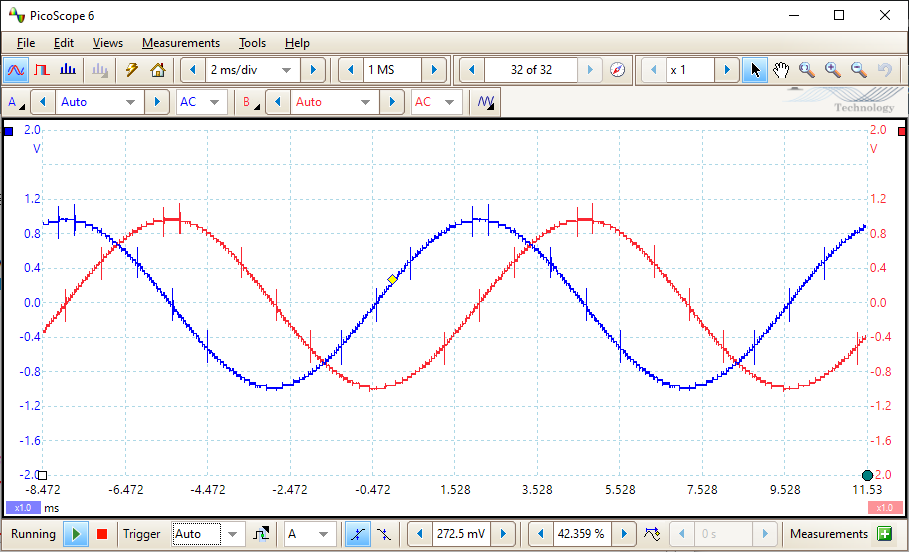
2.2.2. XY View

The XY view of the two channels shows a circle, because the X axis is the voltage of channel A and Y axis corresponds to the voltage of channel B at same time, when channel A is at the peaks the channel B has zero, which is corresponding to X axis at zero.

Showing only channel B would show a straight line on Y axis corresponding to the peak-to-peak amplitude of channel B.

Showing only channel A would show a straight line on X axis.

For ARB1, amplitude is 1, phase of -15 degree, it gives the function $1 \cos (ω t - 15^{\circ})$ .

For ARB2, amplitude is 1.2, phase of 75 degree, it gives the function $1.2 \cos (ω t + 75^{\circ})$ .

2.3. Complex Numbers and MATLAB

The two functions, pol2rec, and rec2pol, are implemented so:

   |function [z] = pol2rec(x)
   |% Polar to rectangular
   |r = x(1);
   |theta = deg2rad(x(2));
 5 |z = r*exp(1i*theta);
   |end
   | 
   |function [x] = rec2pol(z)
   |% Complex number to polar form
10 |x = [abs(z),rad2deg(phase(z))];
   |end

2.4. TIMS and MATLAB Combined

ARB1 is $1 \cos (ω t - 15^{\circ})$ .

ARB2 is $1.2 \cos (ω t + 75^{\circ})$ .

Sum is $1.56 \cos (ω t + 35^{\circ})$ , computed with rec2pol(pol2rec([1,-15])+pol2rec([1.2,75])).
ARB1 is $1 \cos (ω t)$ .

ARB2 is $1.2 \cos (ω t + 180^{\circ})$ .

Sum is $0.2 \cos (ω t + 180^{\circ})$ .
ARB1 is $1 \cos (ω t)$ .

ARB2 is $1.2 \cos (ω t - 180^{\circ})$ .

Sum is $0.2 \cos (ω t + 180^{\circ})$ . It is easy to observe that $1.2 \cos (ω t - 180^{\circ})$ is the same as $1.2 \cos (ω t + 180^{\circ})$ .

2.5. Conjugate Signals

Table 1. Sum of two conjugate signals

Phase (degrees)	Output signal amplitude
0	2.0
30	1.718
60	1.143
90	0
120	1.125
150	1.723
180	2.0
210	1.723
240	1.143
270	0
300	1.125
330	1.718
360	2.0

Figure 4. Plot of Table 1, “Sum of two conjugate signals”

3. Feedback

This lab shows how to use MATLAB to compute with complex numbers. I think MATLAB is not as handy as a good calculator for this task.

However, since most of are already familiar with the subject on complex number, it might be easier if go straight to the SPF experiment part.